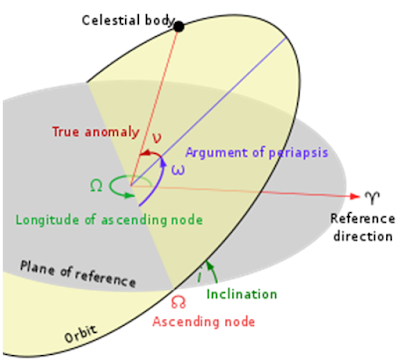
In order to understand the motion of celestial objects, it's necessary to set standard parameters to define orbits. In fact, any orbit can be defined by 6 parameters, known as the 6 orbital elements:
- $a$: length of the semi-major axis
- $e$: eccentricity
- $i$: inclination
- $\Omega$: right ascension of the ascending node
- $\omega$: argument of periapsis
- $v$: true anomaly / time of periapsis passage (also designated with $\theta$)
 |
| Looks confusing, but we'll walk through it together |
1. Length of the Semi-Major Axis ($a$)
This one is easy. If all orbits are ellipses, we'd want to know how wide the orbit is
2. Eccentricity ($e$)
Eccentricity is a measure of how much a given conic section deviates from being circular. It's defined as $e = \frac{c}{a}$, where $c$ is the focal length (length from the center to one of the foci) and $a$ is the line connecting the focus to the semi-minor axis
 |
| The above diagram shows an ellipse with eccentricity of 0.8 |
We learned from the previous section that circles have an eccentricity of 0, ellipses between 0 and 1, parabolas equal to 1, and hyperbolas greater than 1. So for ellipses, the higher the eccentricity, the more stretched out it is
I'll go ahead and introduce the concept of nodes, since we'll need them for the next orbital element anyway. The two nodes are the two points in a satellite's orbit which intersect the Earth's equatorial plane. One is called the ascending node (when the satellite is travelling from the southern to the northern hemisphere) and the other is called the descending node
3. Inclination ($i$)
Inclination is the angle between the orbital plane of the satellite and the equatorial plane
I'll go ahead and introduce the concept of nodes, since we'll need them for the next orbital element anyway. The two nodes are the two points in a satellite's orbit which intersect the Earth's equatorial plane. One is called the ascending node (when the satellite is travelling from the southern to the northern hemisphere) and the other is called the descending node
I'll discuss this again in the section on types of orbits, but orbital inclinations can be classified in to three general categories:
- Prograde orbit: $0^\circ < i < 90^\circ$ (moving eastward at ascending node)
- Polar orbit: $i = 90^\circ$ (moving due north at ascending node)
- Retrograde orbit: $90^\circ < i < 180^\circ$ (moving eastward at ascending node)
4. Right Ascension of the Ascending Node ($\Omega$)
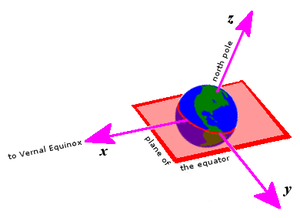
Before we move on, we need to introduce another concept. On Earth, we can easily describe location using latitude, longitude, and altitude. But in space, a satellite's orbit remains fixed relative to the stars while the Earth rotates around it. In short, we need to establish a non-rotating 3D coordinate system, referred to as the Geocentric Equatorial Coordinate System
In the above diagram, the X-Y plane lies on the Earth's equatorial plane. Positive X points toward the vernal equinox, which is where the Sun appears to pass the equator on its way north on the first day of spring. The Z direction points upwards through the Earth's North Pole
 |
| Same concept, but with a Sun-centered frame of reference. Think of the vernal equinox as the line originating from the Earth's equator, through the Sun and into space, on Earth's location in its orbit on the first day of spring |
Now that we've established a non-rotating 3D coordinate system, the right ascension of the ascending node is the angle between the X axis (ie the vernal equinox) and the ascending node. It's always measured eastward on the Earth's equatorial plane away from the vernal equinox
 |
| This diagram happened to label the X, Y, and Z axes as i, j, and k, but the right ascension of the ascending node is clearly illustrated |
5. Argument of Periapsis ($\omega$)
The argument of periapsis is the angle between the ascending node and the point of periapsis (closest approach). It's always measured on the orbital plane in the direction of spacecraft motion
Separately, the term periapsis and apoapsis refers to the points of nearest and farthest approach in an orbit. Those are the generic terms, there are special terms depending on the center of orbit (perigee/apogee for an object orbiting Earth, perihelion/aphelion for an object orbiting the Sun, etc)
6. True Anomaly / Time of Periapsis Passage ($v$ / $\theta$)
There are two ways to define a spacecraft's position on its orbit at any time
- True anomaly is the angle between periapsis and the satellite's current position, measured in the direction of motion
- Time of periapsis passage: if you know the last time of periapsis, you can calculate where on its orbit the satellite should be right now
Summary
The 6 orbital elements are often hard to picture with just diagrams, so I recommend watching this video to better visualize them
Can you guess why there have to be exactly 6 orbital elements?
The first two define the shape of the ellipse in 2 dimensions
The next three orient the 2D ellipse in 3-dimensional space
And the last one defines the position of the spacecraft along its 1-dimensional path of motion
