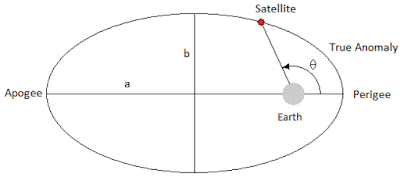
The Three Anomalies
In the section on the 6 orbital elements, I introduced the concept of true anomaly (designated as $v$ or $\theta$), the angle between periapsis and the satellite measured in the direction of satellite motion
True anomaly is a simple and easy way to define the spacecraft's position now, but what if we want to know where it'll be in an hour? This is tricky because we know from Kepler's 2nd law that orbital speeds are faster near periapsis and slower near apoapsis. So we need mean anomaly
Mean anomaly ($M$) can be defined as such: if we were to draw an imaginary circular orbit with the same orbital period as the actual elliptical orbit, mean anomaly is the corresponding angular distance the spacecraft would've traveled on the imaginary circular orbit over the same time
 |
| The shaded areas show that the same area is being swept out by the elliptical and imaginary circular orbits over a given amount of time, but the angles being drawn out are different |
Mean anomaly is useful because there's a mean motion that can solve for the spacecraft's position, given by the equation:
$n = \sqrt{\frac{GM_{Earth}}{a^3}}$
$G =$ Newton's gravitational constant
$M_{Earth} =$ mass of the Earth
$a =$ semi-major axis
Mean motion is nice because it's constant and easy to calculate. It's just the average motion of the satellite in orbit. Now we can calculate mean anomaly at any time:
$M(\Delta t) = n\Delta t + M_0$
$M(\Delta t) =$ new mean anomaly
$n = $ mean motion
$\Delta t =$ change in time
$M_0 = $ original mean anomaly
But who cares about mean anomaly, it's imaginary? It's only useful if we can get back to true anomaly. Unfortunately, that's not an easy task. It takes a helper variable, called the eccentric anomaly
Eccentric anomaly ($E$) can be defined as such: if you went straight up or down from the true anomaly until you intersected the auxiliary circle, the angle between that point, the center, and the periapsis would be the eccentric anomaly
 |
| Eccentric anomaly is given by the angle E in this diagram |
The three anomalies are admittedly very difficult to explain with just words and static pictures, so watch the video below to better visualize (especially starting at 3:38). Notice how all three anomalies line up at periapsis and apoapsis
With all this information, we can now define formulas that can take us between true, eccentric, and mean anomaly. Let $M$ be mean anomaly, $E$ be eccentric anomaly, $v$ be true anomaly, and $e$ be eccentricity
$\cos(E) =\frac{\cos(v) + e}{1+e\cos(v)}$
$M = E - e\sin(E)$
If you're curious to see the derivation of these formulas, check out Wikipedia here, it's quite interesting
The Vis-Viva Equation
Isaac Newton's vis-viva equation defines the instantaneous velocity of a satellite as it coasts in an elliptical orbit around a central body. The formula is given as:
$V = \sqrt{GM(\frac{2}{r} - \frac{1}{a})}$
$V =$ instantaneous velocity
$G =$ Newton's gravitational constant
$M =$ mass of the central body
$r = $ radial distance between the central body and the satellite
$a =$ semi-major axis
Notice that for a circular orbit, we can simplify this equation to just $V = \sqrt{\frac{GM}{r}}$ because $a = r$ at all times
From the earlier section on conics, a satellite reaches escape velocity when its orbit turns into a parabola instead of an ellipse. Since the semi-major axis of a parabola is infinite, the $\frac{1}{a}$ term becomes 0. So escape velocity is given by:
$V = \sqrt{\frac{2GM}{r}}$
And it becomes clear that for any circular orbit velocity, escape velocity from that orbit is given by:
If you're curious to see the derivation of the vis-viva equation, see here
$V_{escape} = V_{circular} \cdot \sqrt{2}$
If you're curious to see the derivation of the vis-viva equation, see here